Tabla de contenidos
En programación, podemos resolver un mismo problema mediante distintos algoritmos. Sin embargo, no todos los algoritmos que resuelven un problema son igual de eficientes al resolverlo.
La notación Big O es un concepto tomado de las matemáticas que se utiliza en ciencias de la computación para describir el rendimiento y escalabilidad de los algoritmos que escribimos.
Es una estimación acerca de cómo pueden crecer los requerimientos de espacio o de tiempo a medida que crece el tamaño de la entrada (inputs) de un algoritmo.
Análisis de Algoritmos
El análisis de algoritmos juega un papel importante en la ciencia de la computación y en la ingeniería de software.
Es fundamental para poder asegurar que las soluciones desarrolladas sean adecuadas, eficientes y escalables para los problemas que intentan resolver.
Cuando estamos desarrollando software, mediante el análisis de algoritmos podemos:
- comparar algoritmos para elegir el más adecuado según cada situación
- encontrar un equilibrio entre el uso de memoria y la velocidad, un aspecto crucial en dispositivos con memoria limitada
- identificar cuellos de botella o áreas de ineficiencia y encontrar maneras de optimizar dichas áreas
- garantizar que el software desarrollado cumple con los requisitos de rendimiento y puede manejar las cargas esperadas en producción
- etc.
El Algoritmo más Eficiente
La eficiencia de un algoritmo depende de su consumo de recursos en las circunstancias específicas en las que se va a utilizar.
Cuando hablamos de recursos, solemos centrarnos en 2 tipos de recursos:
- tiempo (tiempo de ejecución)
- espacio (espacio en memoria)
La notación Big O es una medida teórica que proporciona una estimación de cómo aumenta el tiempo de ejecución o el espacio utilizado en memoria a medida que aumenta el tamaño de la entrada.
¿Por qué Estimar si podemos Medir?

Aunque podríamos medir directamente el tiempo de ejecución o el espacio utilizado, hay varias razones por las cuales usar la notación Big O puede ser más útil:
Independencia del hardware y del software
- El tiempo de ejecución real de un algoritmo puede variar mucho dependiendo del hardware específico (por ejemplo, la CPU, la memoria, el disco) y el software (sistema operativo, compilador, lenguaje de programación) utilizados.
- La notación Big O nos proporciona una medida que es independiente de estas variaciones.
Enfoque en el peor de los casos
- Frecuentemente estamos interesados en el peor de los casos, es decir, el tiempo de ejecución más largo o la mayor cantidad de espacio que un algoritmo puede requerir.
- Esto es especialmente importante para las aplicaciones que necesitan manejar grandes conjuntos de datos.
- Aunque un algoritmo puede ser más rápido que otro para un tamaño de entrada pequeño, puede ser mucho más lento que el otro algoritmo para un tamaño de entrada grande.
Simplificación de la comparación de algoritmos
- La notación Big O nos permite comparar algoritmos de una manera que es fácil de entender y comunicar.
- En lugar de tener que lidiar con medidas de tiempo o espacio exactas y potencialmente complejas, podemos hablar simplemente en términos de O(1), O(n), O(n^2), etc.
El análisis de algoritmos nos permite a los programadores tomar decisiones informadas sobre qué algoritmo utilizar, basándonos en la cantidad de datos con los que necesitamos trabajar y los recursos disponibles.
Notación Asintótica

La notación Big O es una notación asintótica.
En matemáticas la notación asintótica se utiliza para representar el comportamiento de una función cuando su argumento tiende hacia el infinito.
En el contexto de los algoritmos, se utiliza para describir el rendimiento de un algoritmo a medida que el tamaño de la entrada se acerca al infinito.
El Peor caso, el caso Promedio y el Mejor caso
El análisis de algoritmos del peor caso, del caso promedio y del mejor caso se refiere a la evaluación de la eficiencia de un algoritmo en diferentes escenarios.
- El peor caso se refiere a la máxima cantidad de tiempo o espacio que un algoritmo requerirá para una entrada dada.
- El caso promedio considera todas las posibles entradas y calcula la eficiencia media del algoritmo.
- El mejor caso se refiere al escenario más favorable, donde el algoritmo tiene el mejor rendimiento posible.
La notación Big O se utiliza para describir el comportamiento del algoritmo en el peor caso.
Otros tipos de Notaciones Asintóticas
Además de la notación Big O, existen otras notaciones asintóticas utilizadas en el análisis de algoritmos, como la notación Big Omega (Ω) y la notación Big Theta (Θ).
- La notación Big Omega se utiliza para describir el rendimiento de un algoritmo en el mejor caso.
- La notación Big Theta se utiliza para describir el rendimiento de un algoritmo en el caso promedio.
Complejidad Temporal y complejidad Espacial
La complejidad temporal se refiere a la cantidad de tiempo que un algoritmo tarda en ejecutarse.
La complejidad espacial se refiere a la cantidad de memoria que un algoritmo necesita para ejecutarse.
Ambos son factores importantes en la elección de un algoritmo adecuado para una tarea dada.
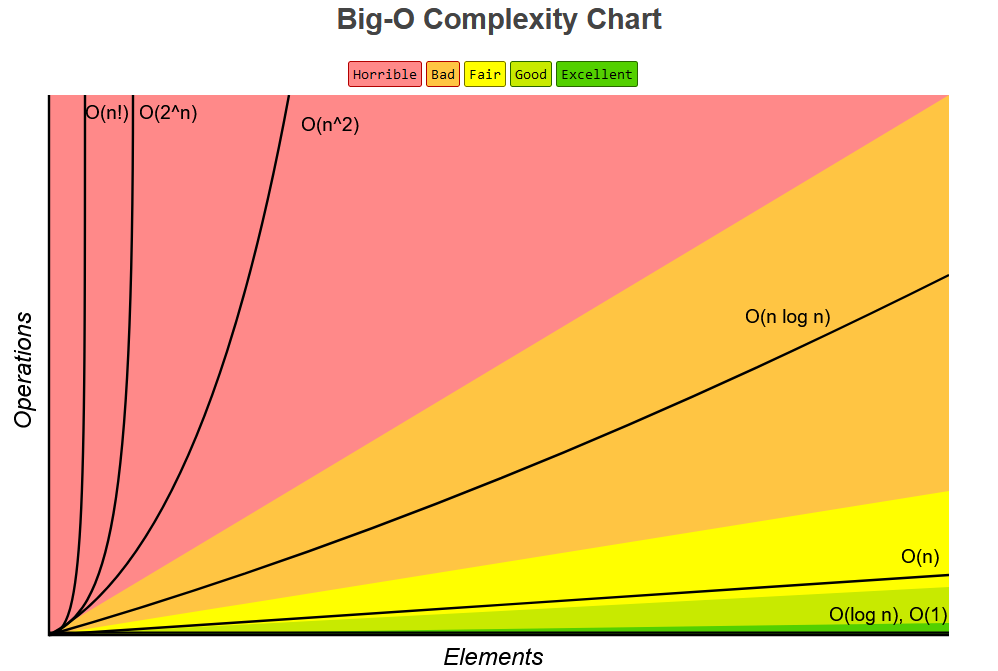
Al graficar la complejidad de los algoritmos mediante la notación Big O:
- en el eje y se representa la cantidad de operaciones realizadas para procesar la entrada del algoritmo
- en el eje x se representa la variable n
La variable n
La variable n representa el tamaño de la entrada del algoritmo, lo que nos informa acerca de cuántos elementos o datos está procesando el algoritmo.
Por ejemplo, si estamos ordenando una lista de números, n sería el número de elementos en esa lista. Si estamos buscando un elemento específico en una lista, n también representaría el número de elementos en esa lista.
En otros contextos, podría representar el número de nodos en un grafo, el número de caracteres en una cadena de texto, entre otros.
Al analizar la eficiencia de un algoritmo, queremos saber cómo se comporta en función del tamaño de su entrada. Por ello, utilizamos n para variar ese tamaño y observar cómo se afecta el comportamiento del algoritmo. Por ejemplo:
- O(1): La eficiencia del algoritmo no depende del tamaño de la entrada. Es una eficiencia constante.
- O(n): La eficiencia del algoritmo es directamente proporcional al tamaño de la entrada. Si duplicas el tamaño de la entrada (2n), el tiempo de ejecución también podría duplicarse aproximadamente.
- O(n^2): La eficiencia del algoritmo es proporcional al cuadrado del tamaño de la entrada. Si duplicas el tamaño de la entrada, el tiempo de ejecución podría cuadriplicarse.
Órdenes de Complejidad
La notación Big O representa el orden de complejidad del tiempo de ejecución (o el espacio requerido) de un algoritmo en función del tamaño de la entrada.
El «orden de complejidad» es una escala comparativa.

Piensa en el crecimiento de una planta. Si te digo que una planta crece «en el orden de centímetros al año», lo que te estoy indicando es que, en general, cada año, puedes esperar que esa planta crezca algunos centímetros.
No te estoy diciendo exactamente cuántos centímetros crecerá cada año, solo te doy una idea general de su tasa de crecimiento.
De manera similar, si decimos que un algoritmo tiene una «complejidad lineal«, esto significa que el tiempo que toma ejecutarse crece linealmente respecto al tamaño de la entrada.
Si duplicas el tamaño de la entrada, puedes esperar, de manera general, que el tiempo de ejecución también se duplique. Sin embargo, no estamos especificando exactamente cuánto tiempo toma el algoritmo con un tamaño de entrada particular.
Por lo tanto, la notación Big O nos permite realizar una estimación de cómo el rendimiento de un algoritmo se ve afectado a medida que el tamaño de su entrada cambia, sin entrar en mediciones específicas.
Los órdenes de complejidad más comunes en la notación Big O son:
O(1): Constante
- Este es el caso ideal, ya que el consumo de recursos (tiempo de ejecución o espacio en memoria), no cambia con el tamaño de la entrada.
- Un ejemplo de esto es acceder a un elemento de un array por su índice.
O(log n): Logarítmico
- El consumo de recursos aumenta logarítmicamente con el tamaño de la entrada. Esto significa que, a medida que n crece, el tiempo de ejecución no crece de forma lineal, sino que se incrementa cada vez más despacio.
- Un ejemplo de un algoritmo que tiene esta complejidad temporal es la búsqueda binaria.
O(n): Lineal
- El consumo de recursos aumenta linealmente con el tamaño de la entrada.
- Un ejemplo es la complejidad temporal del algoritmo de búsqueda lineal, que recorre cada elemento de la lista hasta encontrar el elemento buscado.
O(n log n): Lineal logarítmico
- El consumo de recursos aumenta linealmente y logarítmicamente con el tamaño de la entrada.
- Esto indica que el tiempo de ejecución crece proporcionalmente al tamaño de entrada n, pero se ve moderado por un factor logarítmico.
- Un ejemplo de un algoritmo con esta complejidad temporal es el algoritmo de ordenación por mezcla (merge sort).
O(n^c): Polinómica
- El consumo de recursos crece con la potencia del tamaño de la entrada. En esta notación, c es una constante (O(n^2), O(n^3), etc).
- Por ejemplo, si un algoritmo toma un tiempo de ejecución de O(n^2), se dice que tiene una complejidad temporal cuadrática (uno de los casos de complejidades polinómicas), porque el tiempo de ejecución crece al cuadrado de n.
- En general, los algoritmos con complejidad polinómica son menos eficientes a medida que n crece, y pueden volverse impracticables para valores muy grandes de n.
- Un ejemplo es la complejidad temporal del algoritmo de ordenación bubble sort (complejidad cuadrática O(n^2)) .
O(c^n): Exponencial
- El consumo de recursos crece de manera exponencial con el tamaño de la entrada, lo que hace que estos algoritmos sean impracticables para entradas grandes.
- En esta notación, c es una constante mayor que 1.
- En general, los algoritmos con complejidad exponencial son los menos eficientes y se vuelven impracticables con conjuntos de datos incluso moderadamente grandes.
- Un ejemplo es la secuencia Fibonacci resuelta mediante recursividad.
O(n!): Factorial
- El tiempo de ejecución o el espacio requerido crece de manera factorial con el tamaño de la entrada.
- Los algoritmos con complejidad factorial se consideran extremadamente ineficientes y sólo son viables para tamaños de entrada muy pequeños.
- Un ejemplo es la complejidad temporal del algoritmo de generación de todas las permutaciones posibles de un conjunto de datos.
Limitaciones
La notación Big O es una herramienta esencial en el análisis de algoritmos, pero tiene algunas limitaciones que debemos tener en cuenta:
Ignora constantes y términos más pequeños
- Al analizar el rendimiento de un algoritmo en notación Big O, las constantes y los términos más pequeños se ignoran, centrándose solo en el término de mayor crecimiento.
- Esto significa que dos algoritmos con el mismo orden de Big O podrían tener rendimientos muy diferentes para inputs del mismo tamaño.
Suposiciones sobre el modelo de la máquina
- La notación Big O supone un modelo abstracto de una máquina de computación y no toma en cuenta las realidades de las arquitecturas de hardware modernas.
- Detalles como el uso de memoria caché, la concurrencia, la paralelización o las operaciones de disco pueden tener un impacto significativo en el rendimiento del mundo real que no se refleja en el análisis de la notación Big O.
Caso peor, promedio y mejor
- La notación Big O se usa para describir el peor de los casos de tiempo de ejecución, pero esto podría no ser representativo del rendimiento típico del algoritmo.
- En algunos casos, el peor caso puede ser extremadamente raro, y el caso promedio o incluso el mejor caso pueden ser más relevantes para el análisis.
No tiene en cuenta el costo de las operaciones
- La notación Big O cuenta el número de operaciones, pero todas las operaciones se consideran iguales.
- En la práctica, diferentes operaciones pueden tener costos muy diferentes, y este detalle se pierde en el análisis de la notación Big O.
Por estas razones, aunque la notación Big O es una herramienta valiosa para analizar algoritmos, no debería ser el único factor a considerar al decidir qué algoritmo utilizar.
También se deben tener en cuenta factores como el rendimiento en la práctica, el entorno de hardware y software, el tamaño y la naturaleza del input, y el uso de memoria, entre otros.
Conclusión
Considerar el rendimiento de nuestros algoritmos es importante, ya que puede tener un gran impacto en el rendimiento de nuestras aplicaciones.
La notación Big O es una herramienta sumamente útil para esta tarea ya que nos proporciona una estimación acerca de cómo pueden crecer los requerimientos de espacio o de tiempo a medida que crece el tamaño de la entrada (inputs) de un algoritmo.
Escribí este artículo como resumen de lo que aprendí al estudiar este tema. Espero que te sea útil a ti también para entender mejor qué es la notación Big O y la utilidad que nos ofrece en el análisis de algoritmos.
En un próximo artículo me centraré en desarrollar ejemplos prácticos de cómo utilizarla. 🤓
